In Stitches

After doing the back-stitching on a few of the letters in this counted cross stitch pattern, I wondered if there would always be an even amount of stitches in the outline of a block shape.

Problem:

Define a "block shape" as any shape that can be created by coloring in squares on graph paper. Each square in a multi-square block shape must share at least one side with another square in that shape. Call the length of a square on the graph paper one unit. Prove or disprove: the perimeter of a block shape will always be an even number of units.


Solution:

I will prove that the perimeter is always an even number of units using the Principle of Mathematical Induction.

• Base case: consider a one-square block shape. Its perimeter is 4 units - one for each side. Since 4 is even, the proposition holds for the base case.


• Inductive hypothesis: assume that a block shape consisting of n squares has an even perimeter.


• Deductive step: What happens when I add a square to the n-block shape?
  
  
  
  • If the new square is touching exactly one other square, then I am taking away 1 unit from the perimeter and adding 3 units. That's a net gain of 2 units, so the perimeter remains even.
  
  
  • If the new square is touching exactly two other squares, I am taking away 2 units and adding 2 units to the perimeter. The net change is 0, so the perimeter remains even.
  
  
  • If the new square is touching exactly three other squares, I am reducing the perimeter by 3 units and adding 1. The net loss is 2 units, so the perimeter remains even.
  
  
  • If the new square is touching exactly four other squares, I am taking away 4 units from the perimeter and adding none. The perimeter remains even.
  
  In each possible case, the perimeter of the (n+1)-block shape remains even.

Therefore, by the Principle of Mathematical Induction, the perimeter of a block shape will always be even.

Solution...

Hide solution.

S.A.Tricky

Here's an S.A.T. problem that stumped my students and me (for a little while).

Problem:

a - b = 10
a² - b² = 50

Find b.

Solution:

My instincts were to look for a connection between (a - b)² and a² - b², but it's really much simpler than that. Solve for a in terms of b in the first equation, and substitute into the second equation.

---

Edit: The original post contained a mistake. (10 + b)² = 100 + 20b + b², not 100 + 2b + b².

Solution...

Hide solution.

IDEAs

Here's another S.A.T. problem.

Problem:

In the correctly worked addition problem to the left, A, B, D, E, I, and S each represent a different digit. What is the smallest possible value of D?


Solution:

You don't need to know what every digit in the problem is. You only need to know which digits have to be assigned to which letters in order for the addition problem to work.

Starting in the one's column, E + A = A, or E + A = A + a carry digit. The most two one-digit numbers can add to is 18, so the carry digit would have to be 10. If E + A = 10 + A, then E = 10, but we know that E < 10 (all of the variables are single digits). Thus, E + A = A, and E = 0. Filling that value into the puzzle we get: The value of A doesn't matter. We can forget about the two right-most columns of the addition and look at two left columns. B + S = 10I + D. The most that B and S can add up to is 17 (with B and S equaling 9 and 8), and the least they can sum to is 3 (if B and S equal 1 and 2). However, if B + S < 10, I = 0. We can't have another 0, so B + S must be greater than 10. Therefore, I = 1. Since we've used up 0 and 1, smallest digit we have left for D is 2. We can use 4 for B and 8 for S to make B + S = 12. If we use these values to fill in the puzzle, it all adds up. The smallest number D can be is 2.

Solution...

Hide solution.

Prime Factorization

This problem comes form Project Euler. I solved it with a computer program written in C++.

Problem:

What is the largest prime factor of the number 600851475143?

Solution:

It is tempting to write a function to find the prime factorization of a given number. Why? Because it's cool. I wrote that function, too, but I'm only going to cover the process of solving the given problem.

When solving a programming problem, you should always start on paper to get an idea of what your algorithm needs to do. Suppose I wanted to find the largest prime factor of 90, or what if I wanted to find the largest prime factor of 260? I might do something like what I did in the diagram to the right. In words, our algorithm might look something like this:

Start with your number.
Keep dividing by its factors until you find the biggest prime.

How is the computer going to know which numbers to try? We'll be using a loop, so we can start at 2 and work our way up through the numbers. The computer's factorization of 260 would look more like this: 13/7 is less than 2, 13/8 is even smaller, and 13/9 is smaller still. We're not going to get any more numbers that go evenly into 13 once our divisor is greater than 13/2. We can stop dividing whenever the divisor is greater than half of the number we're dividing. Notice that 4 divides 260, but it did not come up in our list of factors. Instead, we divided 2 out twice. 2 is prime, and 4 is not. Our algorithm automatically sifts out composite numbers by dividing their prime factors out first. In words, our algorithm looks something like this:

Start with your number.
Divide it by 2.
If it divides evenly, keep dividing by 2, otherwise, try 3.
If it divides evenly, keep dividing by 3, otherwise, try 4.
Keep dividing this way until your divisor is greater than or equal to half the original number.

Now we're ready for pseudo-code:

from ( divisor = 2 until divisor >= number/2 )
{
  if ( number is divisible by divisor ) then
    number <- number/divisor
  else
    increment divisor
}
return number

We would like to save our selves some time by only using prime numbers, but we don't have a list of primes. However, we do know that 2 is the only even prime number, so after trying 2, we only have to try odd numbers, which cuts our list of divisors in half. This is my final code:

unsigned long long LargestPrimeFactor(unsigned long long number)
{
  int divisor = 2;
  while(divisor<=sqrt((float)number))
  {
    if(number%divisor==0)
    {
      number = number/divisor;
    }
    else if(divisor==2)
    {
      divisor++;
    }
    else
    {
      divisor+=2;
    }
  }
  return number;
}

The largest prime factor of 600851475143 is 6857.

Solution...

Hide solution.

Atari Space

My friend Justin was reminiscing about some Atari-aged video games: Subspace/Continuum. The problem they inspired reminds me more of Asteroids.

Problem:

A turret in a video game can rotate but not change location. It shoots bullets that travel with a constant velocity V_B. An asteroid travels at a constant velocity V_A. Where should the turret aim to hit the asteroid?

Solution:

You'll never find where you're going if you don't know where you started. Let's put the turret at the center of a Cartesian plane. Add a point A for the asteroid at (x₀, y₀), and add a point for the eventual collision at (x₁, y₁). Label the distances traveled by the asteroid and the bullet D_A and D_B. Recall that little ditty: "Distance = Rate × Time." We can use this whenever we are dealing with constant velocities. I've already labeled arrows R_A and R_B to represent the rates in the diagram.(I'm listing the equation numbers (abbreviated "eqn") on the left. When I use those equations later, I'll show which equation number I used on the right.) Note: the bullet and the asteroid travel for the same amount of time once the bullet is fired, so T has the same value in each equation.

We have two equations and three unknowns, so we'll need to find some more relationships. I can find more information about D_A and D_B by breaking the distances into their horizontal and vertical components. I've added these components to the diagram below.Let β be the angle that the bullet's trajectory makes with the x-axis, and call the angle that the ship flies at with respect to the x-axis α.With all of these variables in play, let's take a moment to recap what is known and what we need to find.Now, we need to trade our variables down to get rid of some of those unknowns. I'll start with x₁. Now do the same with the sines to get rid of y₁. Now that we've gotten rid of x₁ and y₁, solve for T in equation 11 and substitute into equation 15... ...and simplify. Now we're down to one unknown: β. To find β, solve for sin(β), square both sides, and substitute 1 - cos²(β) for sin²(β). Then, use the quadratic equation to solve for the possible values of cos(β), and convert those values into the angles we want. Once we have β, we use equation 18 to find T and equations 4 and 5 to find x₁ and y₁.

I'm not going to attempt to finish this solution unless someone asks me to. I'm too likely to make a mistake somewhere in the tangled mass of algebra that is to follow, and Justin has access to math software that can do the manipulations for him. Comment if you have any questions.

Solution...

Hide solution.

S.A.T. Inequalities

This one comes right out of the S.A.T.s.

Problem:

Each of the following inequalities is true for some values of x EXCEPT

Solution:

The process of elimination is perfect for this problem. A quick look eliminates (A) as a possibility. Anyone could think of a value for x that would make (A) true; for instance, if x = 2, then x² = 4 and x³ = 8, so we can cross of choice (A).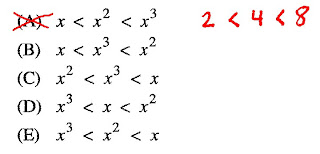
What other kinds of numbers are there? What numbers are "tricky"? Fractions and negatives. If x = 1/2, then x² = 1/4 and x³ = 1/8. That fits with the last inequality, so we can cross off choice (E).
Letting x = -2 makes x² = 4 and x³ = - 8. Ordering those gives us x³ < x < x², so we can cross off choice (D).
Now we only have two possibilities left, and they both look kind of goofy. If you were running out of time on the S.A.T.s, you could just guess between the two earning an expected value of 3/8 of a point, but we're not running out of time. We've tried positive integers, negative integers and fractions, so what's left: negative fractions. If x = -1/2 then x² = 1/4 and x³ = -1/8. That lines up as x < x³ < x², just like choice (B).
Therefore, the only inequality that will not be true for a value of x is choice (C).

Solution...

Hide solution.

Squares of Triangles

Pythagoras was a Greek philosopher and mathematician who lived in the sixth century B.C.E. He acquired a following in his time, and there was a cult built up around him in which he was worshiped as a demi god¹. Today, he is most well known for his contribution to Euclidian geometry: the Pythagorean Theorem. Today's challenge is to prove the Pythagorean Theorem.

Problem:

Given any right triangle ABC, prove A² + B² = C² using only simple geometric formulas. (No trigonometric functions allowed).

Solution:

This problem seeped into my head as I was trying to fall asleep some nights ago, and I never could solve it lying in bed in the dark. It wasn't until I sat down with a pencil and paper and studied the problem from several different angles (during the second and third quarters of the Superbowl) that I came up with a solution.

The first thing I did was to redraw the diagram like this:
That way, I could visualize the quantities, A², B² and C² as the areas of the squares made from the sides of the triangles.

Next, I started to think about this:
Maybe we can find a relationship between a square with the side lengths of A + B and the grey square with lengths C.

The final thing you need to know is that the area of a triangle is equal to half the base times the height: The answer becomes clear when you draw in the rest of the triangles. Look at the red square.The lengths of each of its sides are equal to A + B, so it has the area (A + B)².

If you look at the triangles shaded in pink......you should see that each has a height of A and a base of B, so their areas are ½AB. Therefore, the area of the grey square is equal to the area of the red square from above minus the areas of the four triangles.

Solution...

Hide solution.

Weighing in on Icy Roads

Problem:

Does increasing your vehicle's mass increase your maneuverability on icy roads? Assume the vehicle and all contents are treated as a point mass.

Solution:

It all comes down to two things: momentum and friction. Momentum (p) = the mass of the car (m) times the car's velocity (v), which is a term for a directed speed. We can change momentum by applying a force for a duration of time. Change in momentum = force × time.

Δp = F⋅t
Δm⋅v = F⋅t

What kind of force are we talking about? When it comes to driving a car, it's almost entirely related to the force of friction. When you apply the breaks, you're using
the friction between the tires and the road to stop the car. When you turn the wheel, it's the friction between the tires and the car that will ultimately change your direction, and when you accelerate, without the friction between the road and the tires, you'd just be spinning your wheels.

The force of friction (F_f) = the normal force (F_n) times the coefficient of friction (μ). The normal force of any object is equal to the product of the objects mass, the acceleration due to gravity, and the cosine of the angle (θ) between the horizontal and the surface providing the friction.

F_f = F_n⋅μ
F_f = m⋅g⋅cos(θ)⋅μ

Now, let's look at the change in momentum due to the force of friction applied over time t:

Δp = F⋅t
Δm⋅v = F_f⋅t
Δm⋅v = F_n⋅μ⋅t
Δm⋅v = m⋅g⋅cos(θ)⋅μ⋅t

The m on each side of the equation represents the same thing: the mass of the vehicle plus contents. Dividing each side by m gives us:

Δv = g⋅cos(θ)⋅μ⋅t

Thus, taken as a point mass, the mass of your vehicle has no effect on your ability to change your direction or speed.

Solution...

Hide solution.

Welcome to J-Function Problem Solving

Here's the deal: you send me math or science problems, and I'll post solutions up to as often as one per day. I'll solve problems from any of the subject areas I tutor and also from logic or philosophy. Ask away.

Solution...

Hide solution.