This one comes right out of the S.A.T.s.
Problem:
Each of the following inequalities is true for some values of x EXCEPT
Solution:
The process of elimination is perfect for this problem. A quick look eliminates (A) as a possibility. Anyone could think of a value for x that would make (A) true; for instance, if x = 2, then x2 = 4 and x3 = 8, so we can cross of choice (A).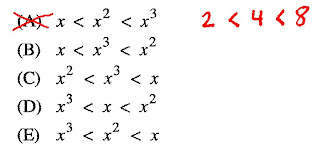 What other kinds of numbers are there? What numbers are "tricky"? Fractions and negatives. If x = 1/2, then x2 = 1/4 and x3 = 1/8. That fits with the last inequality, so we can cross off choice (E).
What other kinds of numbers are there? What numbers are "tricky"? Fractions and negatives. If x = 1/2, then x2 = 1/4 and x3 = 1/8. That fits with the last inequality, so we can cross off choice (E). Letting x = -2 makes x2 = 4 and x3 = - 8. Ordering those gives us x3 < x < x2, so we can cross off choice (D).
Letting x = -2 makes x2 = 4 and x3 = - 8. Ordering those gives us x3 < x < x2, so we can cross off choice (D). Now we only have two possibilities left, and they both look kind of goofy. If you were running out of time on the S.A.T.s, you could just guess between the two earning an expected value of 3/8 of a point, but we're not running out of time. We've tried positive integers, negative integers and fractions, so what's left: negative fractions. If x = -1/2 then x2 = 1/4 and x3 = -1/8. That lines up as x < x3 < x2, just like choice (B).
Now we only have two possibilities left, and they both look kind of goofy. If you were running out of time on the S.A.T.s, you could just guess between the two earning an expected value of 3/8 of a point, but we're not running out of time. We've tried positive integers, negative integers and fractions, so what's left: negative fractions. If x = -1/2 then x2 = 1/4 and x3 = -1/8. That lines up as x < x3 < x2, just like choice (B). Therefore, the only inequality that will not be true for a value of x is choice (C).
Therefore, the only inequality that will not be true for a value of x is choice (C).
Thursday, March 27, 2008
S.A.T. Inequalities
Solved by
J Function
at
11:02 AM
![]()
Labels: Inequalities, S.A.T.s
Subscribe to:
Post Comments (Atom)
2 comments:
Good one. Inequalities confuse a lot of people for some reason. Throw in fractions and they're ready to switch to a liberal arts major.
Math/Science major: What makes the universe work?
Engineering Major: How can we use that to improve our lives/technology?
Business Major: How can we make money of it?
Liberal Arts Major: You want fries with that?
Ha! Good one.
Post a Comment